Tan 2x is equal to minus cot x 5 by 3 299870

Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Get stepbystep solutions from expert tutors as fast as 1530 minutes Your first 5 questions are on us!Y = tan 2 x y = 1 cos x 1 − cos x c o s − 1 (3 x ) c o s − 1 (2 y ) = (2 θ ), then the value of 4 x 212xy cos (2 θ ) 9 y 2 is equal to Hard View solution > tan − 1 (2 1 tan 2 A) tan − 1 (cot A) tan − 1 (cot 3 A) =

How Do You Verify The Identity Cot X Csc X 1 Csc X 1 Cot X Socratic

Tan 2x is equal to minus cot x 5 by 3

Tan 2x is equal to minus cot x 5 by 3-(x 5)(x − 5) = x 2 − 25 The significance of an identity is that, in calculation, we may replace either member with the other We use an identity to give an expression a more convenient form In calculus and all its applications, the trigonometric identities are of central importance On this page we will present the main identities3 Write tanx/sinx as tan(x)/sin(x) 4 Use inv to specify inverse and ln to specify natural log respectively Eg1 Write sin1 x as asin(x) 2 Write ln x as ln(x) 5 Sample Inputs for Practice Eg1 Write (10x2)(x 2) as 10*x2x^2 2 Write cos(x 3) as cos(x^3) 3 Write e x lnx as e

Cot X 2 Cot 2x Tan X Youtube

Trigonometric functions differentiation Derivatives of tan (x) and cot (x) Derivatives of sec (x) and csc (x) Practice Derivatives of tan (x), cot (x), sec (x), and csc (x) Worked example Derivative of sec (3π/2x) using the chain rule Practice Differentiate trigonometric functions Differentiating trigonometric functions reviewFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor Explanation tan2x = 2tanx 1 −tan2x (Trig identity) 2 tan2x = 1 −tan2x tanx = 1 tanx − tan2x tanx = = cotx − tanx Answer link

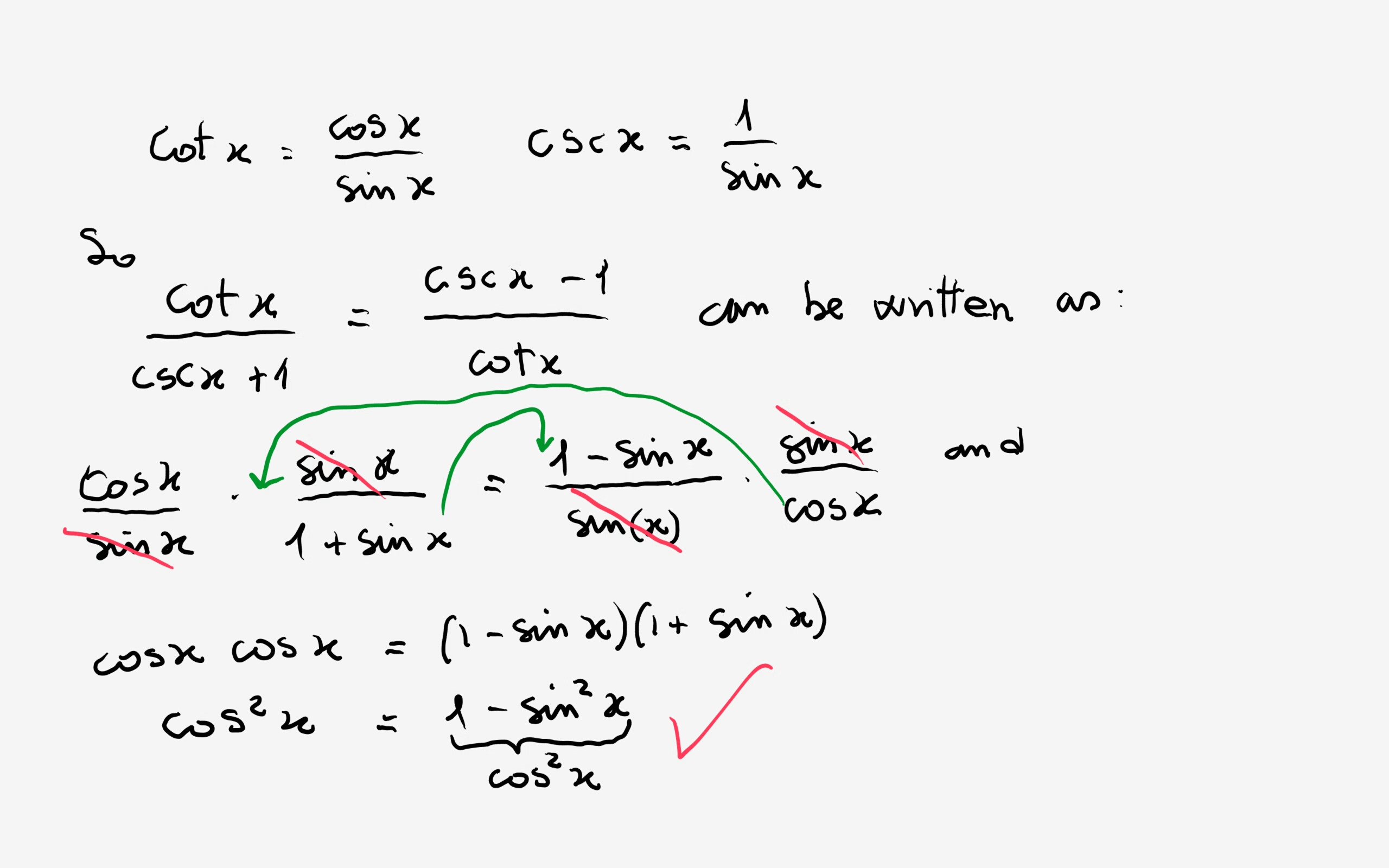
All right So for this exercise, we want to prove or disprove So this means that potentially the identity isn't correct We want to prove or disprove that one over one plus co sign X minus one over one, minus co sign Negative eggs equals negative to co tangent X Cosi connects All right, so for this we're gonna recall that are co tangent identity is equal to co sign x o ver sine x and ourIntegral of tan^2 (x) \square!We are talking about the trigonometric identities in particular to the Pythagorean identities for (tan) and (cot) of (theta), and (sec) and (cosec)0000 Here we are being asked to prove the identity (cot) 2 1 = (cosec) 012 The trick there is to remember the original Pythagorean identity00 Let me write that down to start with, sin 2 x cos 2 x = 1, that is the original Pythagorean

Purplemath In mathematics, an "identity" is an equation which is always true These can be "trivially" true, like "x = x" or usefully true, such as the Pythagorean Theorem's "a 2 b 2 = c 2" for right trianglesThere are loads of trigonometric identities, but the following are the ones you're most likely to see and use Let x = theta, since it's easier to type, and is essentially the same variable Since tan^2(x)=tan(x), you know that tan(x) must either be 1 or zero for this statement to be true So let tan(x)=0, and solve on your calculator by taking the inverse Similarly for, tan(x)=1Cot(x) = 1/tan(x) , so cotangent is basically the reciprocal of a tangent, or, in other words, the multiplicative inverse What is the value of sin inverse sin 3?

What Is 1 Cot X X 1 Tan X Sec X Equal To

Limit X Pi 2 Cotx Cosx Pi 2x 3 Equals

 True Start with the well known pythagorean identity sin^2x cos^2x = 1 This is readily derived directly from the definition of the basic trigonometric functions sin and cos and Pythagoras's Theorem Divide both side by cos^2x and we get sin^2x/cos^2x cos^2x/cos^2x = 1/cos^2x tan^2x 1 = sec^2x tan^2x = sec^2x 1 Confirming that the result is an identityClick here👆to get an answer to your question ️ limit x→pi/2 cotxcosx (pi2x)^3 equalsPlus Gama equals 4/3 And this is a compound angle identity for 10 So using the identity from our formula booklet, this is the same as 10 um, data plus 10 gamma over one minus 10th ada 10 gamma equal 4/3 On we can fill in the sights of 10 data was X 10 gamma is ah one minus X and then one minus 10 Thade is X and tan gamma was one minus

If Tan Cot X Cot Tan X Then Sin 2x Brainly In

Solved Find Sin 2x Cos 2x And Tan 2x From The Given Information Csc 5 Tan X 0

Sin (X 2π) = sin X , period 2π cos (X 2π) = cos X , period 2π sec (X 2π) = sec X , period 2π csc (X 2π) = csc X , period 2π tan (X π) = tan X , period π cot (X π) = cot X , period π Trigonometric Tables Properties of The Six Trigonometric Functions Graph, domain, range, asymptotes (if any), symmetry, x and y Trigonometry Formulas As the name suggests, trigonometry deals with the study of trianglesThe trigonometry concept includes the use of various trigonometry formulas, identities, and laws Trigonometric identities are used across different areas of work such as engineering architecture, stringed musical instruments and other different scientific specializations If you mean sin2(x) cos2(x) then it can be simplified by noting that the square of the sine of x is equal to (1 cos(2x)) ÷

Solve Tan2x Cot X P 3 Brainly In

Solved 2 Cot X 2cotx Tan 2x E Tan 2x Csc X 2 Cos Sin 3 Chegg Com

Trigonometric Simplification Calculator \square! Ex 34, 3 Find the principal and general solutions of the equation cot x = –√3 Given cot x = −√3 tan x = 1/cot⁡𝑥 tan x = 1/(−√3) tan x = (−1)/√3 We know that tan 30° = 1/√3 Since tan x is negative So, x will lie in llnd and lVth Quadrant Value in llnd Quadrant = 180° – 30°Is cot the inverse of tan?

Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions Exercise 5 2 Avail Free Pdf

What Is The Value Of Tan X 1 Cot X Cot X 1 Tan X Quora

Answer (1 of 12) \begin {align*}f (x)&=\cot (x)\tan (x)\\ &=\frac {\cos (x)}{\sin (x)}\frac {\sin (x)}{\cos (x)}\\ &= \frac {\cos^2 (x)\sin^2 (x)}{\sin (x)\cosWhat are the relations among all the trigonometrical ratios of (180° θ)?D is the differential operator, int is the integration operator, C is the constant of integration Identities tan x = sin x/cos x equation 1 cot x = cos x/sin x equation 2 sec x = 1/cos x equation 3 csc x = 1/sin x equation 4

How Do You Verify The Identity Cot X Csc X 1 Csc X 1 Cot X Socratic

Rd Sharma Solutions For Class 11 Chapter 5 Trigonometric Functions Exercise 5 2 Avail Free Pdf

(x2 ¡4x5)¢1¡(x3)¢(2x¡4) (x2 ¡4x5)2 = x2 Just as in the case of tanx, the range of cotx is all real numbers, and this should not be surprising, since essentially cotx is 1 divided by the tangent of x For this same reason, the period of cotx is also where cosx is not equal to 0Answer (1 of 7) So , it's bit easy but since it might be a whole new concept, So sit back and enjoy 1 Basic formulation 2 Concept Though you don't require concept but I'll give the information regarding this , as this is taught us in 12th grade So , tan(x) = tanx We have taken negativeAn older video where Sal finds the derivative of tan (x) using the quotient rule Created by Sal Khan Trigonometric functions differentiation Derivatives of tan (x) and cot (x) Derivatives of sec (x) and csc (x) Practice Derivatives of tan (x), cot (x), sec (x), and csc (x) Worked example Derivative of sec (3π/2x) using the chain rule

Get Out Paper For Notes Ppt Download

2

Tan(x y) = (tan x tan y) / (1 tan x tan y) sin(2x) = 2 sin x cos x cos(2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x) tan(2x) = 2 tan(x) / (1Legend x and y are independent variables, ;Solution of the differential equations cos x dy = y (sin x y)dx, 0 x π/2, is Solution of x sin (y / x) dy = (y sin (y / x) x) dx is Solution Set Of X Equals 3 Modulus 7 P Belongs To Z Is Given By

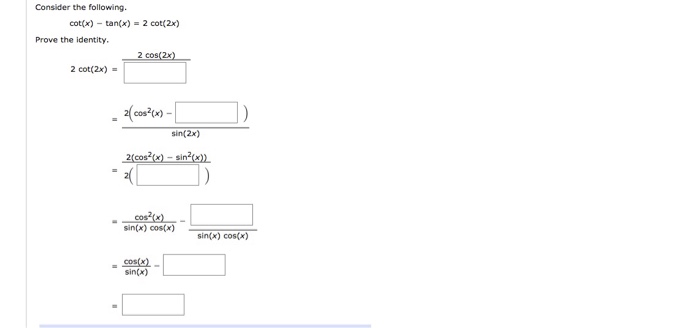
Solved Consider The Following Cot X Tan X 2 Cot 2x Chegg Com

Trigonometric Identities Ppt Video Online Download

Learn how to solve rational equations problems step by step online Solve the equation ln (1/x)ln (2x^3)=ln (486)ln (3) The logarithm of a quotient is equal to the logarithm of the numerator minus the logarithm of the denominator The difference of two logarithms of equal base b is equal to the logarithm of the quotient \log_b (x)\log_b (yThen cot θ = x or, π tan – θ = 2 x ⇒ tan – θ–1 π 2 x = So tan(cot ) tan–1 θ cot –θ cot cot cot(tan )π π –1 –1 2 2 x x x = = = − = The equality is valid for all values of x since tan–1x and cot–1x are true for x ∈ R Example 9 Find the value of sec tan–1 2 y Solution Let tan =–1 θ 2 y, where π π θ ,Find the equation of the tangent line to the curve y equals left parenthesis x minus 3 right parenthesis superscript 7 baseline left parenthesis x plus 1 right parenthesis squaredy=(x−3)7(x1)2 at the point left parenthesis 4 comma 25 right parenthesis(4,25)

Cotangent Function Calculator

Tanx Cotx M Tinh Tan 2 Cot 2x Miny Vn Cộng đồng Hỗ Trợ Học Tập

The Pythagorean Identities are based on the properties of a right triangle cos2θ sin2θ = 1 1 cot2θ = csc2θ 1 tan2θ = sec2θ The evenodd identities relate the value of a trigonometric function at a given angle to the value of the function at the opposite angle tan(− θ)Free math lessons and math homework help from basic math to algebra, geometry and beyond Students, teachers, parents, and everyone can find solutions to their math problems instantlyThe other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions if the argument is regarded as an angle given in radians 7

Solve The Trigonometric Equation Tan 2x Cot X Pi 3 Youtube

Qprove That Tan X 2 Tan 2x 4 Tan 4x 8 Cot 8x Cot X Mathematics Topperlearning Com Blpusg55

Question 6065 Please solve this equation and show me the work I am stumped on this one the square root of 3 times the csc of x minus 2 times the cot of x equals 0 Found 2 solutions by solver, lwsshak32 and the square of the cosine of x is equal to (1 cos(2x)) ÷Find cot1 (25) rounded to four decimal places Solution Let y = cot1 (25) so that cot(y) = 25 Then, tan(y) = 1/25 = 04 We need to solve this equation Remember that there are two solutions a first quadrant angle and a third quadrant angle By calculator, y = or Since the inverse cotangent must be a first or second

Cot X 2 Cot 2x Tan X Youtube

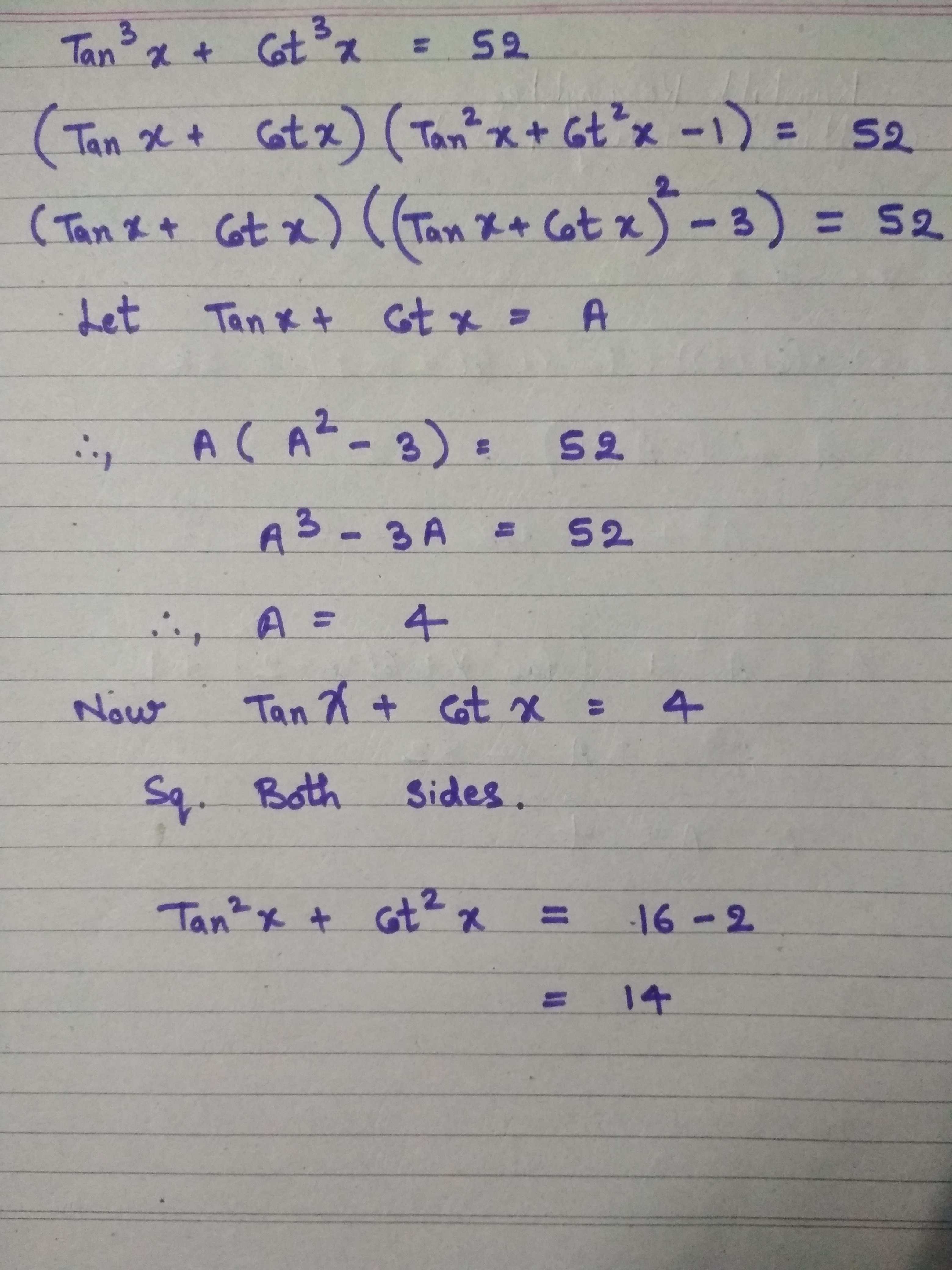
Tan 3x Cot 3x 52 Then What Is The Value Of Tan 2x Cot 2x Askiitians

1 cos(x) ⋅ 1 sin(x) 1 cos ( x) ⋅ 1 sin ( x) Multiply 1 cos(x) 1 cos ( x) and 1 sin(x) 1 sin ( x) 1 cos(x)sin(x) 1 cos ( x) sin ( x) Because the two sides have been shown to be equivalent, the equation is an identity tan(x)cot(x) = sec(x)csc(x) tan ((a) 2cos2 x3sinx =3 0So, we have to change the angle 3 such that it lies between −π2 and π2

Analysis Of Errors In Derivatives Of Trigonometric Functions International Journal Of Stem Education Full Text

3

The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variableFor example, the derivative of the sine function is written sin′(a) = cos(a), meaning that the rate of change of sin(x) at a particular angle x = a is given by the cosine of that angle0 Some common Identities and formulas generally used in finding Trigonometric ratios are stated below Double or Triple angle identities 1) sin 2x = 2sin x cos x 2) cos2x = cos²x – sin²x = 1 – 2sin²x = 2cos²x – 1 3) tan 2x = 2 tan x / (1tan ²x) 4) sin 3x =Trigonometry Sin, Cos, Tan, Cot A circle centered at the origin of the coordinate system and with a radius of 1 is known as a unit circle If P is a point from the circle and A is the angle between PO and x axis then The xcoordinate of P is called the cosine of A and is denoted by cos A;

How To Find The Principle And General Solution Of Tan2x Cot X Pi 3 Mathematics Topperlearning Com 8433

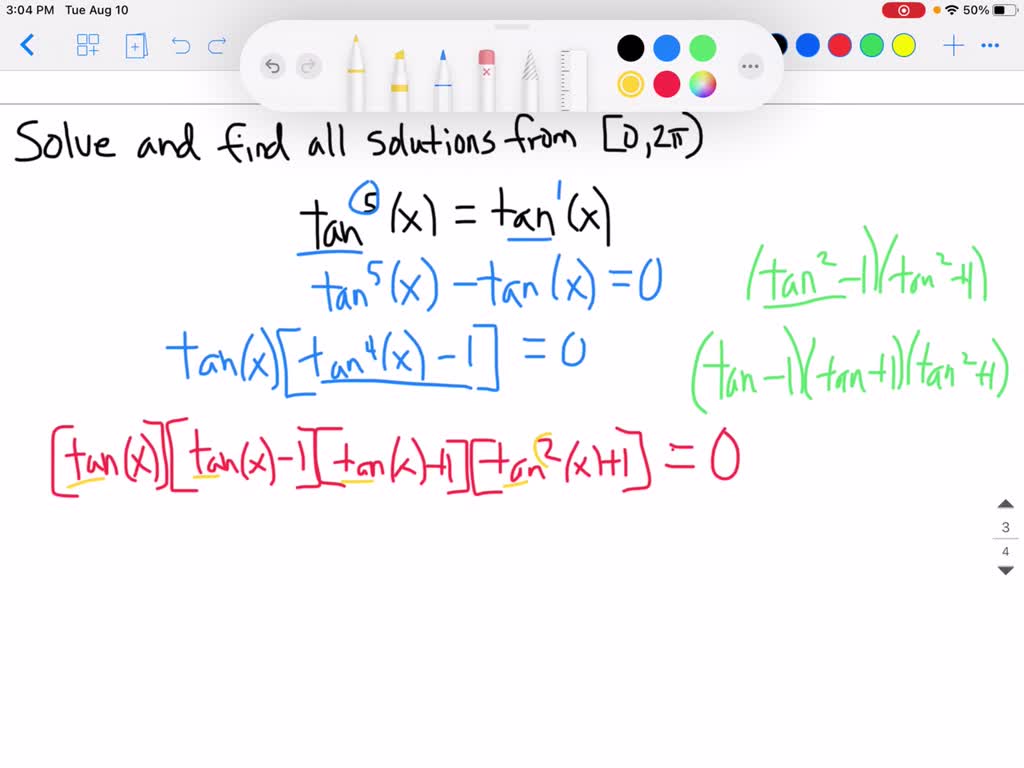
Solved Solve The Equation Find All Solutions Of The Equation In The Interval 0 2d œ Enter Your Answers As A Comma Separated List 5 Tan 2x Aˆ 5 Cot X 0 X

In trigonometrical ratios of angles (180° θ) we will find the relation between all six trigonometrical ratios We know that, sin (90° θ) = cos θ cos (90° θ) = sin θ tan (90° θ) =4) cot2(2x) Answer (3) 2 cot 2x Solution cot x – tan x = (1/tan x) – tan x = (1 – tan 2 x)/tan x Multiplying and dividing by 2, = 2 (1 – tan 2 x)/2 tan x Using the formula tan 2A =Cosx = sinycosx = cos(90° y) x = 90° yx y = 90° (i)cot (x 40°) = tan (50° y)cot (x 40°) = cot (90° 50° y) x 40° = 40° y x y = 80

Solve Tan2x Cot X Pi 3

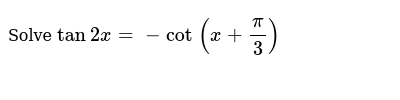
Solve Tan2x Cot X Pi 3

 Transcript Example 7 If cot⁡𝑥 = – 5/12 , x lies in second quadrant, find the values of other five trigonometric functions Since x lies in llnd Quadrant Where cos x and tan x will be negative But sin x will be Positive We know that 1 cot2x = cosec2 x 1 ((−5)/12)^2 = cosec2 x 1 25/144 = cosec2 x (144 25)/144 = cosec2 x 169/144 = cosec2x cosec2 x = 169/144 cosec2 x = 50 /5 heart 7 skmusical18 tan2x=cot (xpi/3)=tan (pi/2xpi/3)=tan (5pi/6x) therefore 2x=npi5pi/6x,nEz X=npi5pi/6,nEz e3radg8

Solved 4 Tan X Cot X Tan 2 X Cot 2 X 2 Sin Chegg Com

Solve Tan2x Cot X P 3 Brainly In

3 2 I Prove That Tan X Cot X Can Never Be Equal To Scholr

Trigonometric Functions Wikipedia

Example 28 If Tan X 3 4 Find Sin X 2 Cos X 2 Tan X 2

Trigonometric Function

1

2

Tanx 4 3 X In Quadrant Ii Find The Value Of Sinx 2 Cosx 2 Tanx 2

Tan2x ただの悪魔の画像

Evaluate Int 4 Cot X 5 Tan X 2 Dx

If Tan X Cot X 2 Find The Value Of Tan 2x Cot 2x

Solve Tan2x Cot X Pi 3 Youtube

Solve Tan2x Cot X Pi 3

What Is The General Solution Of Tan X Cot X 2 Quora

How To Evaluate Lim X 0 Cot X Sin 2x Quora

Limit Limit X Pi 2 Cot X Cos X Pi 2x 3 Equals To Sarthaks Econnect Largest Online Education Community

1

If Cot X 5 12 In Second Quadrant Then Find The Value Of Trigonometric Function Brainly In

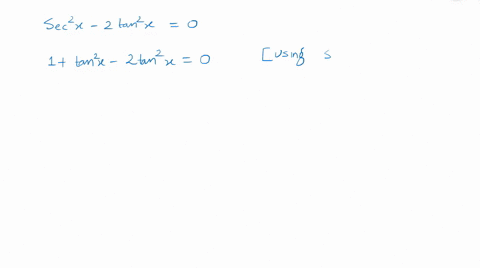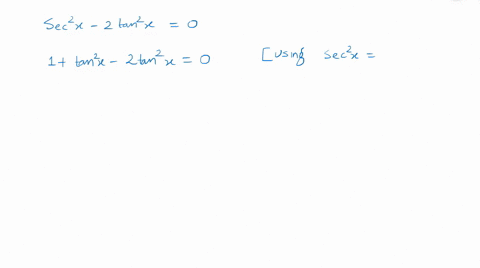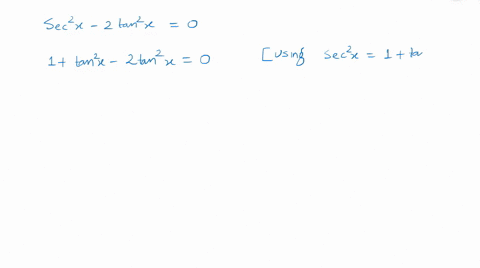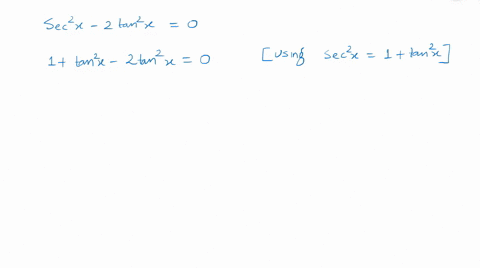
Solved Finding All Solutions In 0 2 Pi Cot X Tan 2 X 3 Pi

Tanx Cotx 2 Sec 2x Cosec 2x Brainly In

Find The General Solution Of Tan X Cot 2x 0

Tanx 3 Cotx 5 Secx Trigonometric Quadratic Equation Test Youtube

Solve Tan2x Cot X P 3 Sarthaks Econnect Largest Online Education Community

Solving The Integral Of Cos X Video Lesson Transcript Study Com

Example 7 If Cot X 5 12 X Lies In Second Quadrant

2

Find Solutions Of Cot X Tan X 4 Cot 2x 0 For X In 0 360 Mathematics Stack Exchange

Prove The Identity Tan X 1 Cot X Cot X 1 Tan X Sec X Cosec X 1 Sarthaks Econnect Largest Online Education Community

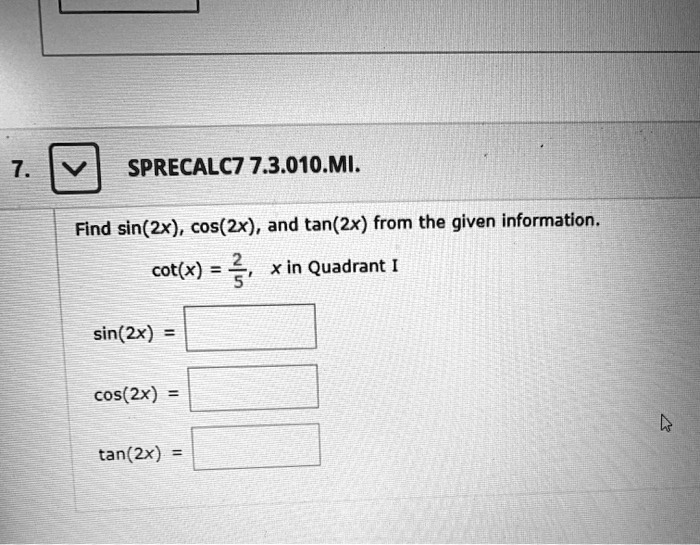
Yewms5xtyqgtbm

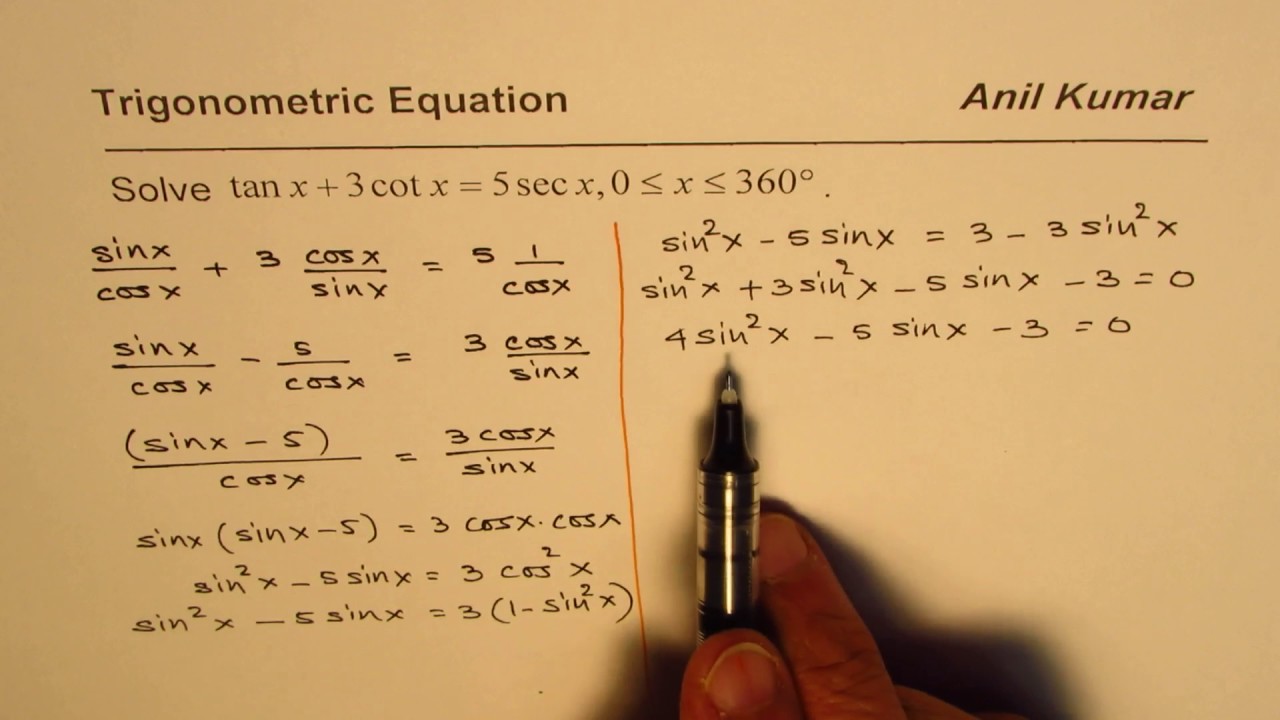
Trig Equation Tanx Plus 3 Cot X Equals 5 Sec X Youtube

Solve This Example 22 Solve Tan 2x Cot X P3 Maths Trigonometric Functions Meritnation Com

Q 5 For All Real Values Of X Cot X 2 Cot 2x Is Equal To A Tan Maths Meritnation Com

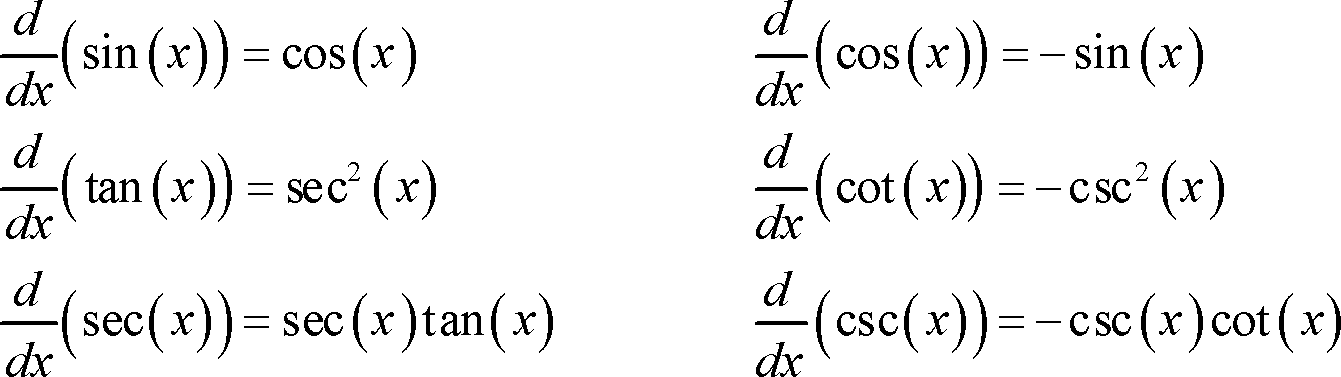
How Do You Find The Derivative Of Y Tanx Cotx Socratic

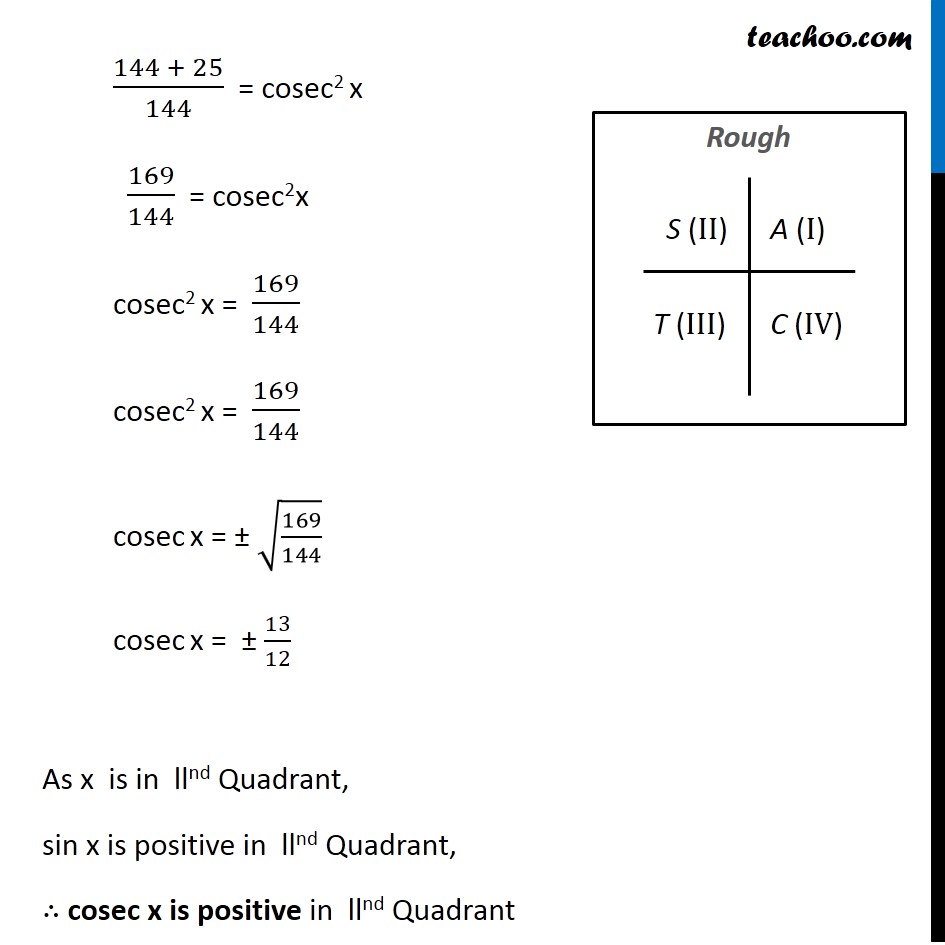
Example 7 If Cot X 5 12 X Lies In Second Quadrant

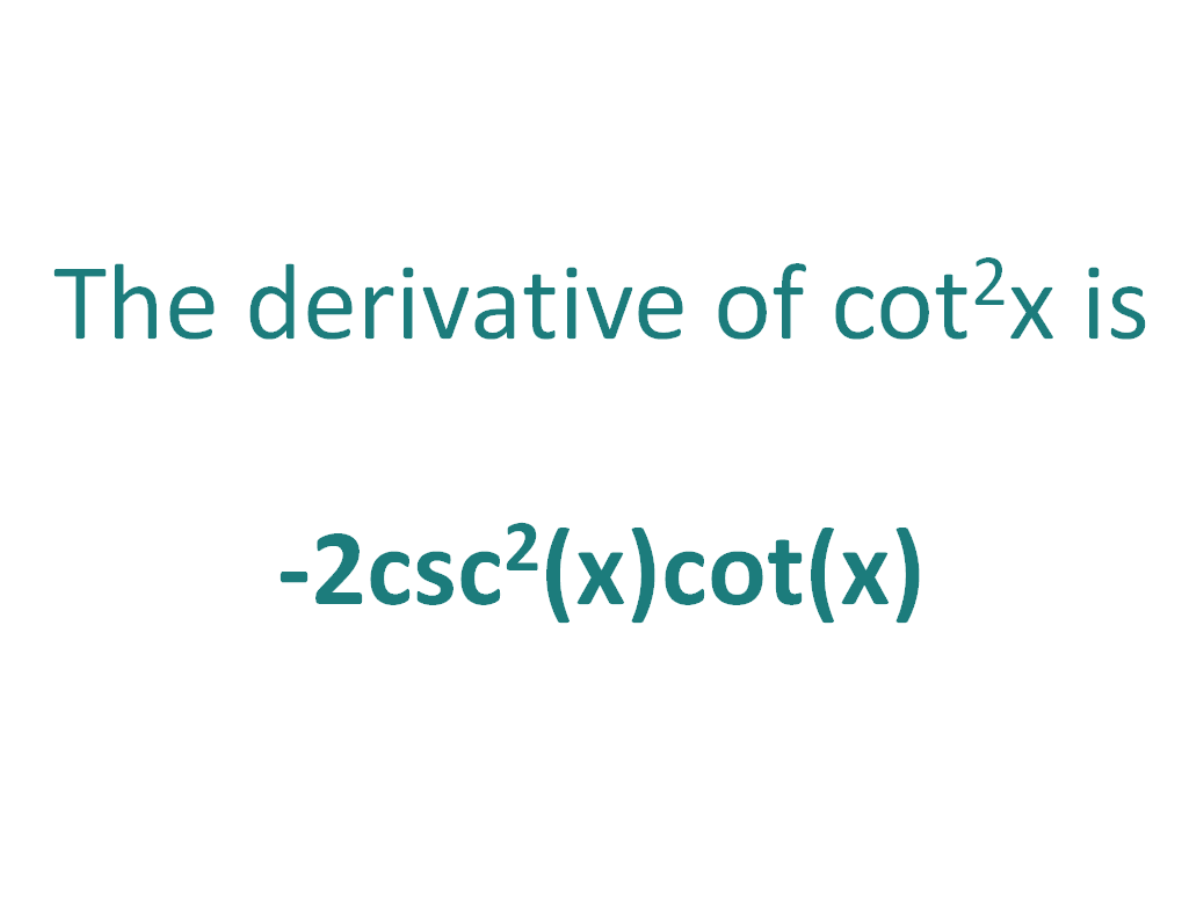
The Derivative Of Cot 2x Derivativeit

Tan 2x Formula What Is Tan 2x Formula Examples

Trigonometry Reciprocal Identities Expii

How Do You Prove The Identity Tan 2x Secx 1 1 Cosx Cosx Socratic

1

Tanx Cotx 5 3 Ise Tan 2x Cot 2x Kactir Lutfen Cozermisiniz Simdiden Tesekkurler Eodev Com

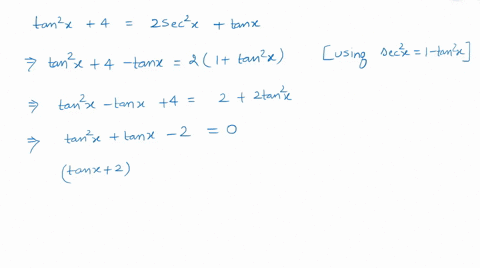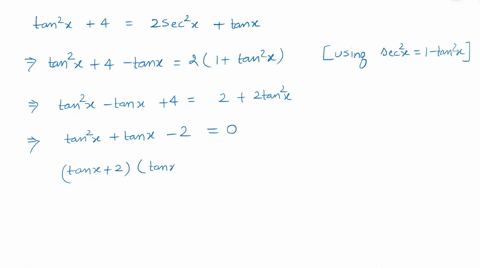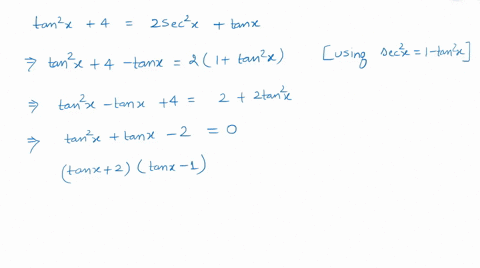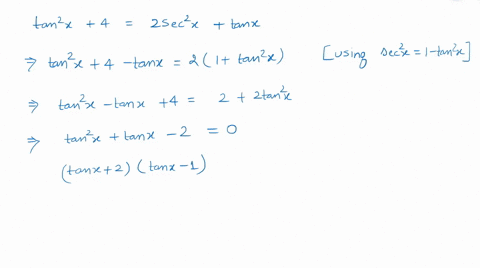
Solved Finding All Solutions In 0 2 Pi Cot X Tan 2 X 3 Pi

If Tan X 2tan 2x 3tan 3x 8cot 8x 3 Then The General Solution Of X

The Squeeze Theorem

If 3 Tan 1 X Cot 1 X P Then X Equals Studyrankersonline

Trigonometric Identities And Equations

Derivatives Of Tan X And Cot X Video Khan Academy

Solved Verify The Given Identity Tan 2x 2 Cot X Tan X Chegg Com

Definite Integral Int Frac Pi 12 Frac Pi 4 Frac 8 Cos2x Tan X Cot X 3 Dx Mathematics Stack Exchange

Cambridge International Examinations Cie Advanced Level Mathematics Pure Mathematics 2 3 By Ayman Alam Issuu

Cot X Cos 2 X Tan X Sin 2 X 2 Cot 2x Youtube

For All Real Values Of X Cot X 2 Cot 2x Is Equal To A Tan 2x B Tan X Sarthaks Econnect Largest Online Education Community

Examples With Trigonometric Functions Even Odd Or Neither Video Lessons Examples And Solutions

Solving Trigonometric Equations With Identities Precalculus Ii

What Is The Value Of Tan X 1 Cot X Cot X 1 Tan X Quora

Relating Trigonometric Functions Trigonometry Socratic

Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples

Tan2x Cot X 60 Maths Trigonometric Functions Meritnation Com

Solution Verify The Identity Step By Step Cot3x 1 Tan 2x 3tanx Tan 3x

Tan2x ただの悪魔の画像

If F X Tan X Find F X And Hence Find F Pi4

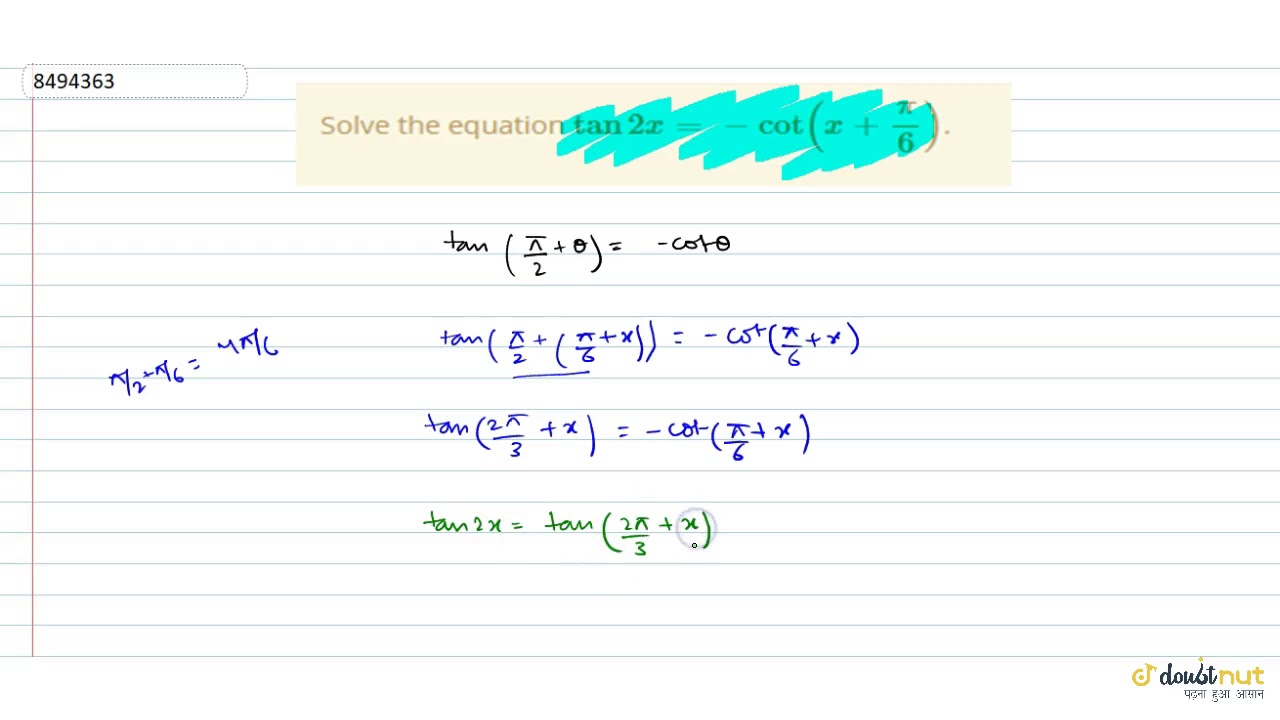
Solve The Equation Tan 2x Cot X Pi 6 Youtube

Trigonometry Solutions Manual

If Tan X Cot X 2 Then What Is The Value Of Sin X Quora

What Is The General Solution For Tanthanx Tan 2x Tan 3x Quora

Find The Derivative Of The Given Function Y Tan 2x 1 Cot 2x I Tried Converting The Original Function In Terms Of Sin And Cos But It Was Still Too Complicated To Be Called Simplified

Solved Verify The Identity Tan2 X Cot2 X Tan X Cot X Tan Chegg Com

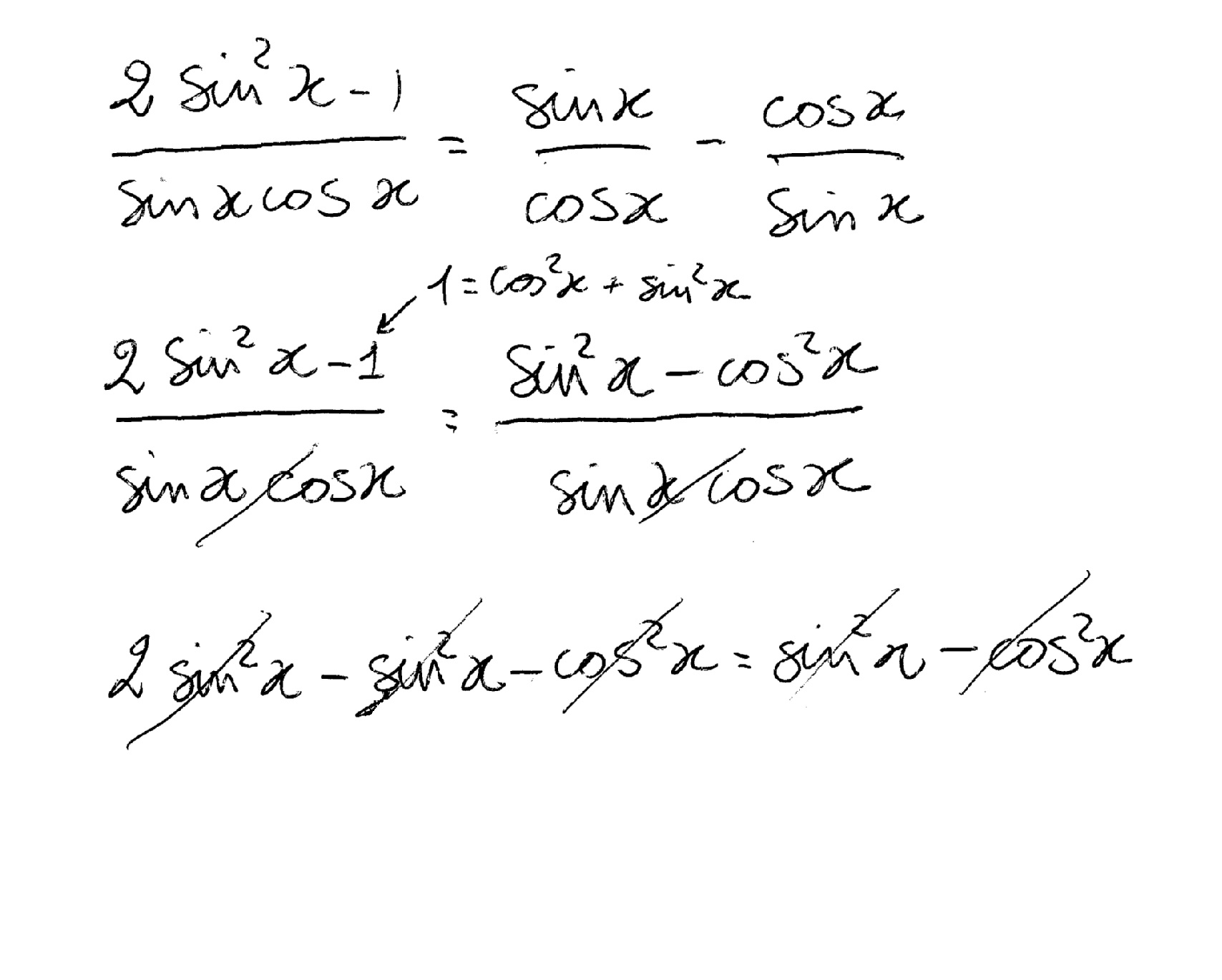
How Do You Prove 2sin 2x 1 Sinxcosx Tanx Cotx Socratic

Ex 3 2 3 If Cot X 3 5 Find Values Of Other Trigonometric

Sin X Cos Y Identity Patofia

Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples

Tan2x ただの悪魔の画像

Prove That Tan 3 1 Tan 2x Cot 3x 1 Cot X 1 2sin 2xcos 2x Sinx Cosx Maths Trigonometric Functions Meritnation Com

If Tan 1 X Tan 1 Y 4p 5 Then Cot 1x Cot 1y Equals Studyrankersonline

2

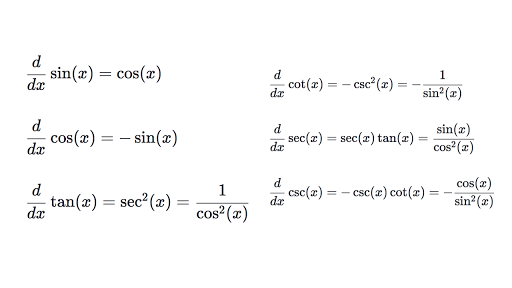
Differentiating Trigonometric Functions Review Article Khan Academy

Example 22 Solve Tan 2x Cot X Pi 3 Teachoo Examples

Tangent Half Angle Formula Wikipedia